1 条题解
-
0
P1761 正方形 题解
1. 思路分析
注意到题目中的正方形都是旋转 后的,计算此时正方形与 轴交点的坐标并不简单,还带着无理数 ,非常不方便。由此,我们可以引入一个我自定义的词汇:“斜边长”。
我们再把输入给定的正方形边长想象成它的“斜边长”,我们的坐标的单位长度也就按照“斜边长”更改为 啦。
好了,烦人的 由此被我们解决掉了。不要忘了我们定义“斜边长”的目的是什么:计算此时正方形与 轴的交点。
显然,稍作观察即可发现,每个正方形的坐标都跟它左边相邻的正方形有直接的关系。
给出递推公式:
但,只跟它左边的正方形有关系吗?并不是的。还是样例给的好:
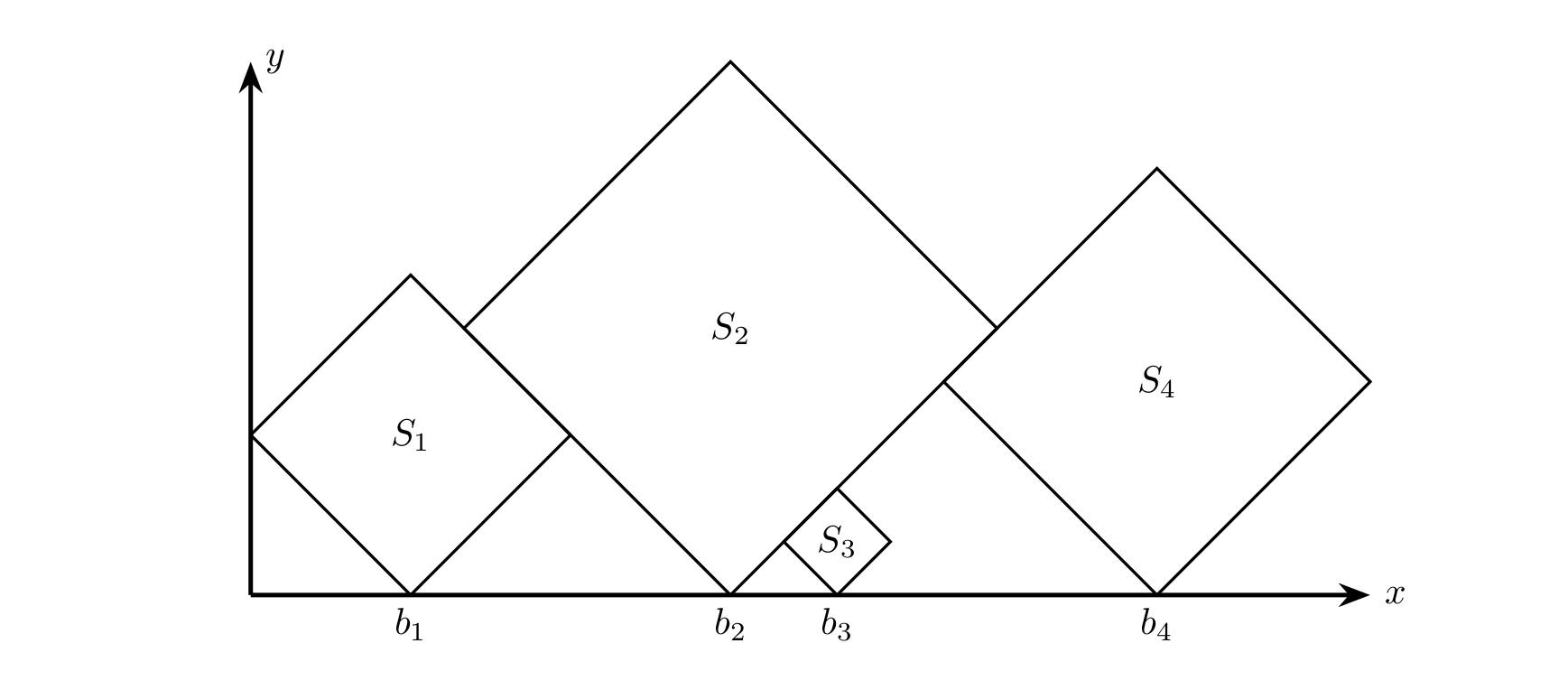 正方形的坐标如果只看 的话, 将与 相等,显然不合题意。问题出现在了 身上。稍加分析即可发现,每个正方形的坐标都跟它左边所有的正方形有直接的关系。
正方形的坐标如果只看 的话, 将与 相等,显然不合题意。问题出现在了 身上。稍加分析即可发现,每个正方形的坐标都跟它左边所有的正方形有直接的关系。给出递推公式:
$$pos_i = \max_{j = 1}^{i - 1} pos[j] + \min\{a_i,a_j\}$$再构造几组数据,加以验证这是正确的。
坐标都求完了,应当去判断哪些正方形会被其它正方形覆盖掉了。
有了上面的经验,就知道不能再只看左边相邻的和右边相邻的了,需要看左边所有的和右边所有的。
每个正方形都有一个最左和最右的端点,也就是 和 。
我们记 为第 个正方形右侧“斜边长”比它长的正方形中左端点最靠左的下标。同理,记 为第 个正方形左侧“斜边长”比它长的正方形中右端点最靠右的下标。
我们只需要判断 是否大于等于 即可。如果是的话,则输出 即可(注意: 初始化为 , 初始化为 )。
但是,我们需要再细心一点:如果没有找到合适的正方形使得 与 更新呢?换句话说, 与 如果还是 与 呢?其实,我们最后还需要走两步:
- 把 和 取 。
- 把 和 取 。
这样我们就能放心的写代码了!
2. 代码实现
相信我在上述的讲解中已经很明确地给出了代码细节了。
自认为码风良好。#include <bits/stdc++.h> using namespace std; const int maxn = 60; const double inf = 1e5; int n, a[maxn], pos[maxn]; double div(int x) { if (x & 1) return (x >> 1) + 0.5; return x >> 1; } bool check(int x) { double l = inf, r = -inf; for (int i = 1; i < x; i++) { if (a[i] < a[x]) continue; r = max(r, (double) pos[i] + div(a[i])); } for (int i = x + 1; i <= n; i++) { if (a[i] < a[x]) continue; l = min(l, (double) pos[i] - div(a[i])); } r = max(r, (double) pos[x] - div(a[x])); l = min(l, (double) pos[x] + div(a[x])); if (r >= l) return false; return true; } int main() { ios::sync_with_stdio(false); cin.tie(0); cout.tie(0); while (cin >> n && n) { memset(pos, 0, sizeof(pos)); for (int i = 1; i <= n; i++) { cin >> a[i]; if (i == 1) pos[i] = (a[i] + 1) >> 1; else for (int j = 1; j < i; j++) pos[i] = max(pos[i], pos[j] + min(a[i], a[j])); } for (int i = 1; i <= n; i++) if (check(i)) cout << i << " "; cout << "\n"; } return 0; }
这是本蒟蒻的第一篇题解,可能问题有点多,请管理员通过。(QwQ)
信息
- ID
- 735
- 时间
- 1000ms
- 内存
- 125MiB
- 难度
- 7
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
